The Steiner Circumellipse -
Two Simple Methods of Construction
by
Markus Heisss
2019/2022/2024
Würzburg, Bavaria
The copying of the following graphics is allowed, but without changes.
[To get a bigger picture, please click it with the cursor.]
A Short Introduction to the Topic:
First step: Construct a circle at centroid G
with the radius of the minor semi-axis.
Now draw three lines parallel to the major
semi-axis of the ellipse
through the vertices of the triangle.
Three of the intersections form an equilateral triangle.
See next figure:
Fig. 1: Affine transformation of the Steiner circumellipse
Here we have a case of an affine transformation,
which is described in detail in Roger A. Johnson's important classic book
"Advanced Euclidean Geometry"
in the chapter "Vertical Projections" (p. 290ff).
Strongly simplified: Think a cut along the major
semi-axis
vertical to the plane of the ellipse,
as shown in the next figure:
Fig. 2: Vertical cut through the Steiner circumellipse
Simply said: Project the Steiner circumellipse so,
that it becomes a circle, than the original triangle ABC
becomes an equilateral triangle.
The angle Φ between both planes can be simply calculated.
(The formula is shown in the graphic above.)
There is also a connection of this equilateral triangle to the Napoleon triangles.
(More advance information to the Napoleon triangles you get here:
[https://napoleon-triangles.jimdofree.com/]
Theorem:
The outer Napoleon triangle and the equilateral triangle A'B'C',
which is a vertical projection of the Steiner circumellipse,
are homothetic (Heisss, August 2019).
("Homothetic" means, that the triangles are similar
and have the same orientation.
The respective sides of both triangles are therefore parallel).
This is shown in the next graphic:
Fig. 3: Outer Napoleon triangle and into a circle transformed Steiner circumellipse
It exists also a counterpart to the inner Napoleon triangle,
because there are three alternative intersections of the parallel lines with the projected circle.
These three points of intersection form another equilateral triangle.
Theorem:
The inner Napoleon triangle and the equilateral triangle A''C''B'',
which is a vertical projection of the Steiner circumellipse,
are homothetic (Heisss, August 2019).
This is shown in the following graphic:
Fig. 04: Inner Napoleon triangle and into a circle transformed Steiner circumellipse
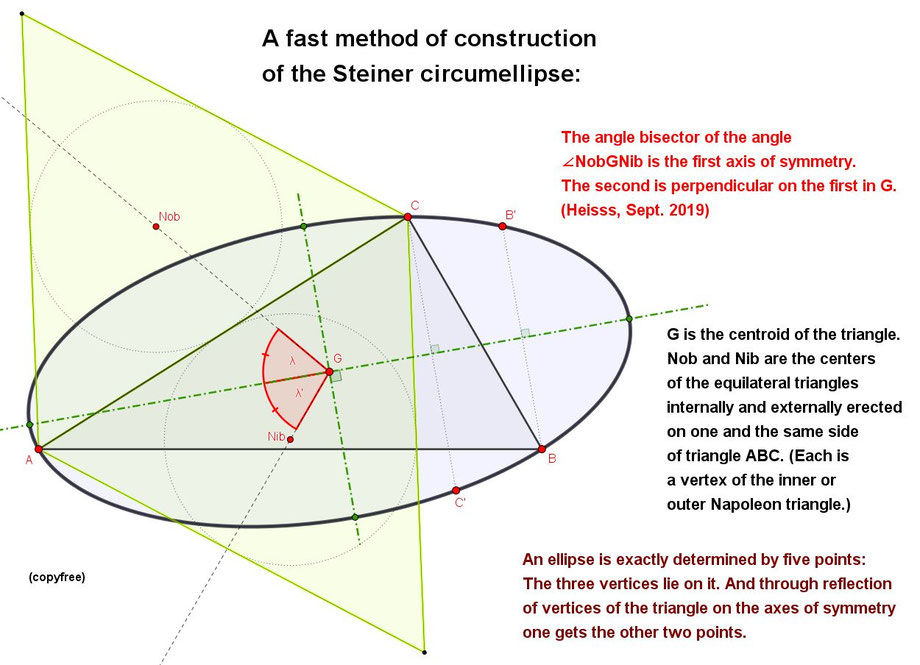
Both theorems together lead to the very simple and "real" method of construction
of the axes of symmetry of the Steiner circumellipse.
As shown above yet, but again:
Fig. 5: Fast Method of Construction of the Steiner circumellipse
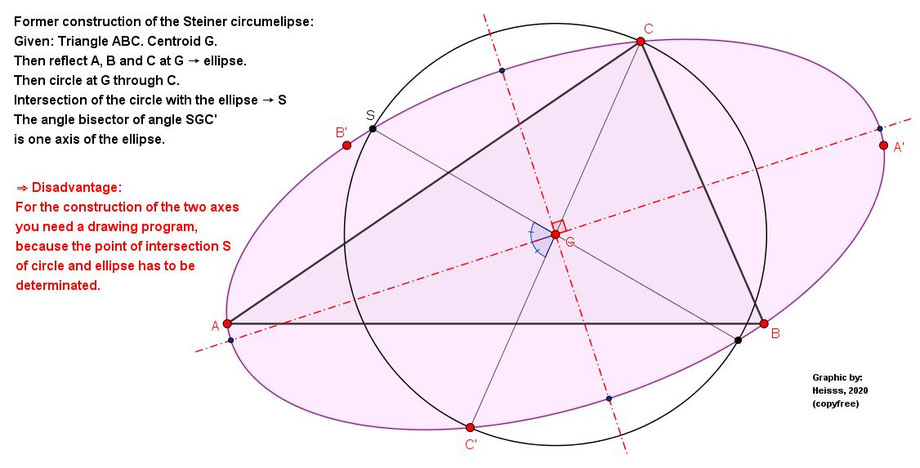
... and in comparison a former method of construction:
Fig. 5a: Former Method of Construction of the Steiner Circumellipse with a Disadvantage
... And Another Method of Construction
The following explanation is illustrated with an example:
You can copy these formulas:
k1=a^2+b^2+c^2, k2=a^2*b^2+b^2*c^2+c^2*a^2, k3=a^4+b^4+c^4, k4=(k3-k2)^(1/2), k5=k1/((2*k2-k3)^(1/2))
ae=1/3*((k1+2*k4)^(1/2)), be=1/3*((k1-2*k4)^(1/2)), tanPhi=1/3*(k5-((k5^2-3)^(1/2)))
Construction step by step:
[Note: Of course it is no pure method of construction with only straight edge and compass.
But the result in the end is exact!]
1st) Construct the triangle ABC and its centroid G.
2nd) Draw a straight line through one of the vertices of the triangle
with the calculated angle φ to the inner side of the triangle.
The intersection of this line with the perpendicular bisector
of the respective triangle side is the Point
P.
3rd) The line GP is one of both axes of symmetry of the Steiner circumellipse.
The second axis of symmetry is perpendicular in the centroid.
4th) Transfer the calculated lengths of the semi-axes ae and be
from the centroid to the respective axis of symmetry of the Steiner circumellipse.
5th) These four points of intersection Qn and the three vertices of the triangle
lie all on the Steiner circumellipse ... which are more than enough points for a drawing.
Fig. 06: Alternative construction of the Steiner circumellipse
By the way: The intersection of the circumcircle of the triangle with the Steiner circumellipse
leads to a further point, the so-called "Steiner point" S.
(... as shown above)
Note: The Steiner point S is the Kimberling center X99.
A table of all important points of a triangle you can find here:
Note: Further important information to the Steiner circumellipse
you will find at the following website:
[http://mathworld.wolfram.com/SteinerCircumellipse.html]
There is also a so-called "Steiner inellipse".
See next graphic:
Fig. 7: The Steiner inellipse
You can see that the respective distances
have always half the lengths of those of the circumellipse.
Further important information to the Steiner inellipse
you will find here:
Closing Note:
The shown "alternative method of construction"
(--which is, as said before, no pure construction--) uses the discovery,
that the intersections of the three McCay circles
with the respective perpendicular bisectors of the triangle's sides
form two collinearities, which are identical
with the axes of symmetry of the Steiner circumellipse.
Application:
With the help of these two methods of construction
it is easy to construct the three McCay circles of a given triangle!
More information in detail you will find here:
... And further relationships to the Steiner circumellipse here:
********************************
Postscript: 2. April 2022
... and another discovery:
Fig. 8: Relationship between the Steiner circumellipse and the two Napoleon circles
Please note also the simple relationships between the radii of the Napoleon circles
and the semi-axes of the Steiner circumellipse!